The topmost node of the tree is called the root, and the nodes below it are called the child nodes. Each node can have multiple child nodes, and these child nodes can also have their own child nodes, forming a recursive structure.

Why Tree is considered a non-linear data structure?

The data in a tree are not stored in a sequential manner i.e., they are not stored linearly. Instead, they are arranged on multiple levels or we can say it is a hierarchical structure. For this reason, the tree is considered to be a non-linear data structure.

Basic Terminologies In Tree Data Structure:

• Parent Node: The node which is an immediate predecessor of a node is called the parent node of that node. {B} is the parent node of {D, E}.
• Child Node: The node which is the immediate successor of a node is called the child node of that node. Examples: {D, E} are the child nodes of {B}.
• Root Node: The topmost node of a tree or the node which does not have any parent node is called the root node. {A} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes of the tree.
• Leaf Node or External Node: The nodes which do not have any child nodes are called leaf nodes. {I, J, K, F, G, H} are the leaf nodes of the tree.
• Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node. {A,B} are the ancestor nodes of the node {E}
• Descendant: A node x is a descendant of another node y if and only if y is an ancestor of x.
• Sibling: Children of the same parent node are called siblings. {D,E} are called siblings.
• Level of a node: The count of edges on the path from the root node to that node. The root node has level 0.
• Internal node: A node with at least one child is called Internal Node.
• Neighbour of a Node: Parent or child nodes of that node are called neighbors of that node.
• Subtree: Any node of the tree along with its descendant.

Representation of Tree Data Structure:

A tree consists of a root node, and zero or more subtrees T₁, T₂, … , T_k such that there is an edge from the root node of the tree to the root node of each subtree. Subtree of a node X consists of all the nodes which have node X as the ancestor node.

Representation of a Node in Tree Data Structure:

A tree can be represented using a collection of nodes. Each of the nodes can be represented with the help of class.

Importance for Tree Data Structure:

One reason to use trees might be because you want to store information that naturally forms a hierarchy. For example, the file system on a computer: The DOM model of an HTML page is also tree where we have html tag as root, head and body its children and these tags, then have their own children. Please refer Applications, Advantages and Disadvantages of Tree for details.

Types of Tree data structures:

Tree data structure can be classified into three types based upon the number of children each node of the tree can have. The types are:

• 1. Binary Tree

  A binary Tree is defined as a Tree data structure with at most 2 children. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.

  Example:
  Consider the tree below. Since each node of this tree has only 2 children, it can be said that this tree is a Binary Tree

  

  Some common types of binary trees include full binary trees, complete binary trees, balanced binary trees, and degenerate or pathological binary trees. Examples of Binary Tree are Binary Search Tree and Binary Heap.

2. Binary Search Tree

A binary Search Tree is a node-based binary tree data structure that has the following properties:

• The left subtree of a node contains only nodes with keys lesser than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• The left and right subtree each must also be a binary search tree.

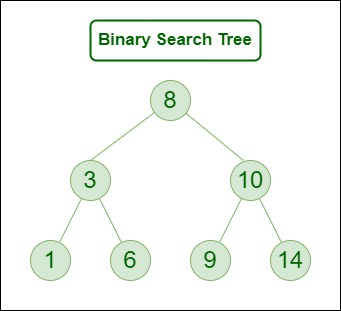
Binary Search Tree

3. AVL Tree

AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees for any node cannot be more than one.

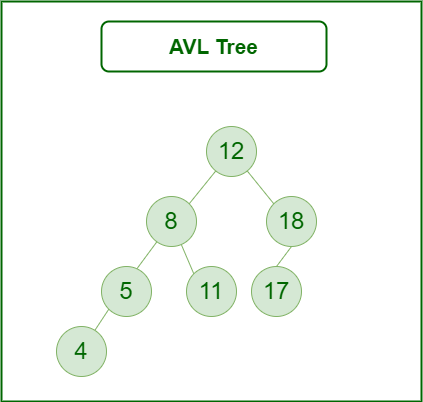
AVL Tree

• Ternary Tree: A Ternary Tree is a tree data structure in which each node has at most three child nodes, usually distinguished as “left”, “mid” and “right”.
• N-ary Tree or Generic Tree: Generic trees are a collection of nodes where each node is a data structure that consists of records and a list of references to its children(duplicate references are not allowed). Unlike the linked list, each node stores the address of multiple nodes.

Basic Operations Of Tree Data Structure:

• Create – create a tree in the data structure.
• Insert − Inserts data in a tree.
• Search − Searches specific data in a tree to check whether it is present or not.

Tree Traversal

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.

If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.

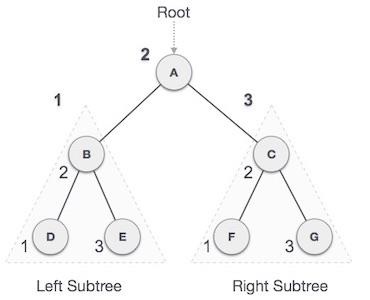
We start from A, and following in-order traversal, we move to its left subtree B.B is also traversed in-order. The process goes on until all the nodes are visited. The output of in-order traversal of this tree will be −

D → B → E → A → F → C → G

Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

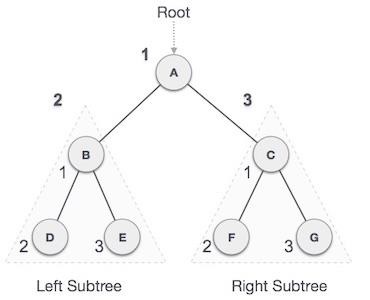
We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be −

A → B → D → E → C → F → G

Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

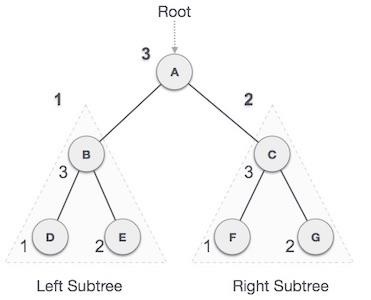
We start from A, and following pre-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be −

D → E → B → F → G → C → A

The first type of self-balancing binary search tree to be invented is the AVL tree. The name AVL tree is coined after its inventor’s names − Adelson-Velsky and Landis.

AVL Trees

In AVL trees, the difference between the heights of left and right subtrees, known as the Balance Factor, must be at most one. Once the difference exceeds one, the tree automatically executes the balancing algorithm until the difference becomes one again.

There are usually four cases of rotation in the balancing algorithm of AVL trees: LL, RR, LR, RL.

LL Rotations

LL rotation is performed when the node is inserted into the right subtree leading to an unbalanced tree. This is a single left rotation to make the tree balanced again −

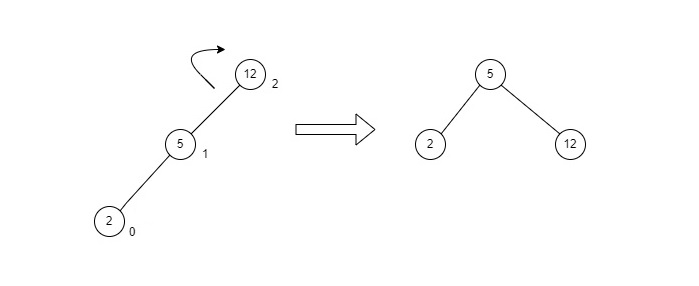
Fig : LL Rotation

The node where the unbalance occurs becomes the left child and the newly added node becomes the right child with the middle node as the parent node.

RR Rotations

RR rotation is performed when the node is inserted into the left subtree leading to an unbalanced tree. This is a single right rotation to make the tree balanced again −

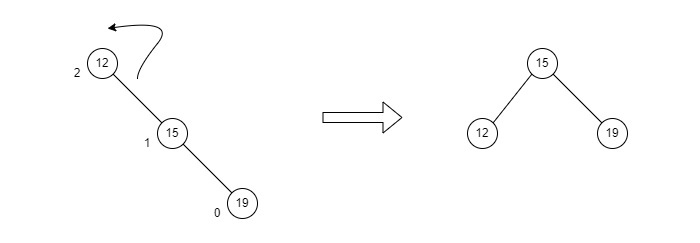
Fig : RR Rotation

The node where the unbalance occurs becomes the right child and the newly added node becomes the left child with the middle node as the parent node.

LR Rotations

LR rotation is the extended version of the previous single rotations, also called a double rotation. It is performed when a node is inserted into the right subtree of the left subtree. The LR rotation is a combination of the left rotation followed by the right rotation. There are multiple steps to be followed to carry this out.

• Consider an example with “A” as the root node, “B” as the left child of “A” and “C” as the right child of “B”.
• Since the unbalance occurs at A, a left rotation is applied on the child nodes of A, i.e. B and C.
• After the rotation, the C node becomes the left child of A and B becomes the left child of C.
• The unbalance still persists, therefore a right rotation is applied at the root node A and the left child C.
• After the final right rotation, C becomes the root node, A becomes the right child and B is the left child.

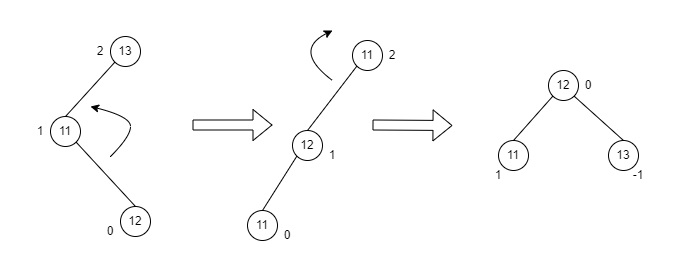
Fig : LR Rotation

RL Rotations

RL rotation is also the extended version of the previous single rotations, hence it is called a double rotation and it is performed if a node is inserted into the left subtree of the right subtree. The RL rotation is a combination of the right rotation followed by the left rotation. There are multiple steps to be followed to carry this out.

• Consider an example with “A” as the root node, “B” as the right child of “A” and “C” as the left child of “B”.
• Since the unbalance occurs at A, a right rotation is applied on the child nodes of A, i.e. B and C.
• After the rotation, the C node becomes the right child of A and B becomes the right child of C.
• The unbalance still persists, therefore a left rotation is applied at the root node A and the right child C.
• After the final left rotation, C becomes the root node, A becomes the left child and B is the right child.

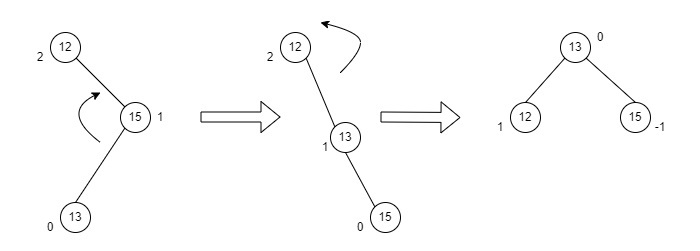
Fig : RL Rotation

Basic Operations of AVL Trees

The basic operations performed on the AVL Tree structures include all the operations performed on a binary search tree, since the AVL Tree at its core is actually just a binary search tree holding all its properties. Therefore, basic operations performed on an AVL Tree are − Insertion and Deletion.

Insertion operation

The data is inserted into the AVL Tree by following the Binary Search Tree property of insertion, i.e. the left subtree must contain elements less than the root value and right subtree must contain all the greater elements.

However, in AVL Trees, after the insertion of each element, the balance factor of the tree is checked; if it does not exceed 1, the tree is left as it is. But if the balance factor exceeds 1, a balancing algorithm is applied to readjust the tree such that balance factor becomes less than or equal to 1 again.

Algorithm

The following steps are involved in performing the insertion operation of an AVL Tree −

Let us understand the insertion operation by constructing an example AVL tree with 1 to 7 integers.

Starting with the first element 1, we create a node and measure the balance, i.e., 0.

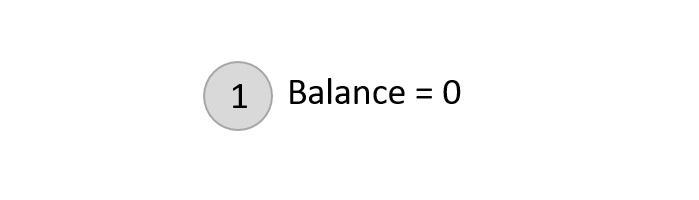
Since both the binary search property and the balance factor are satisfied, we insert another element into the tree.

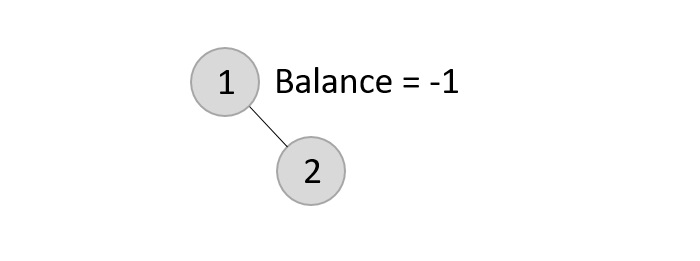
The balance factor for the two nodes are calculated and is found to be -1 (Height of left subtree is 0 and height of the right subtree is 1). Since it does not exceed 1, we add another element to the tree.

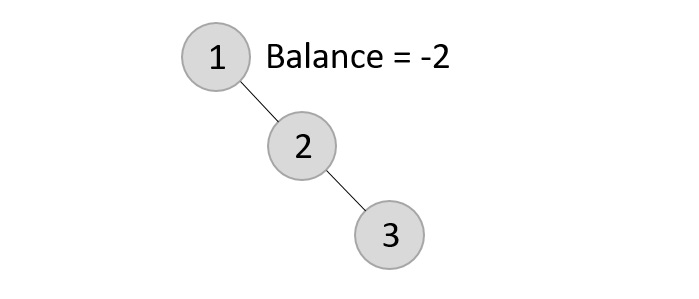
Now, after adding the third element, the balance factor exceeds 1 and becomes 2. Therefore, rotations are applied. In this case, the RR rotation is applied since the imbalance occurs at two right nodes.

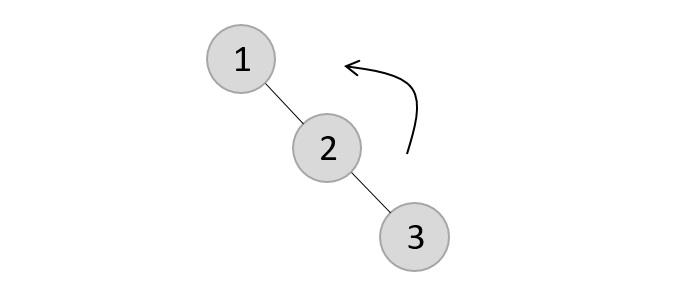
The tree is rearranged as −

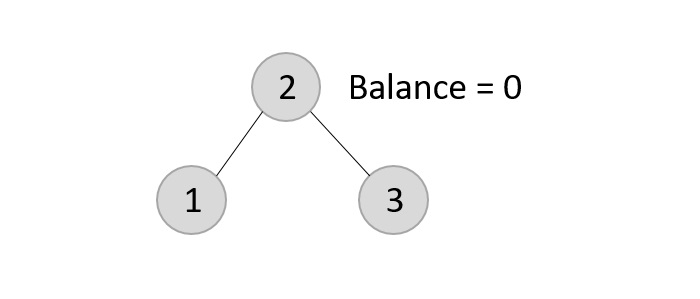
Similarly, the next elements are inserted and rearranged using these rotations. After rearrangement, we achieve the tree as −

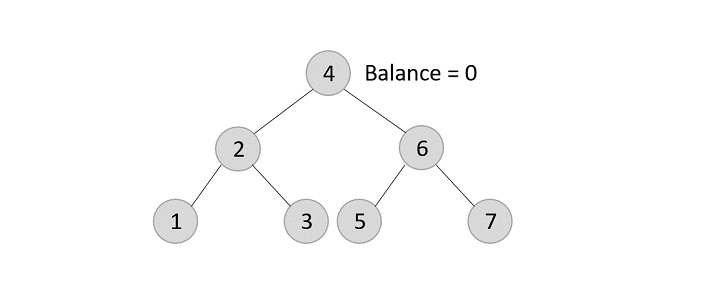
Deletion operation

Deletion in the AVL Trees take place in three different scenarios −

• Scenario 1 (Deletion of a leaf node) − If the node to be deleted is a leaf node, then it is deleted without any replacement as it does not disturb the binary search tree property. However, the balance factor may get disturbed, so rotations are applied to restore it.
• Scenario 2 (Deletion of a node with one child) − If the node to be deleted has one child, replace the value in that node with the value in its child node. Then delete the child node. If the balance factor is disturbed, rotations are applied.
• Scenario 3 (Deletion of a node with two child nodes) − If the node to be deleted has two child nodes, find the inorder successor of that node and replace its value with the inorder successor value. Then try to delete the inorder successor node. If the balance factor exceeds 1 after deletion, apply balance algorithms.

Using the same tree given above, let us perform deletion in three scenarios −

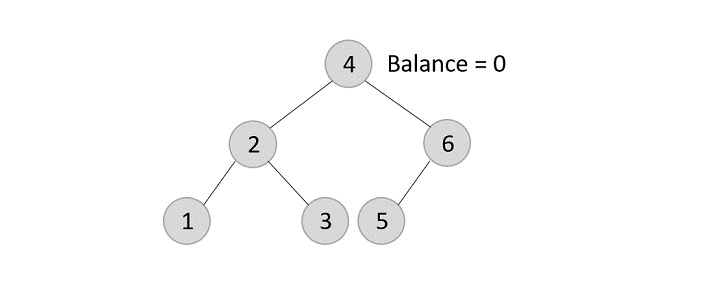
• Deleting element 7 from the tree above −

Since the element 7 is a leaf, we normally remove the element without disturbing any other node in the tree

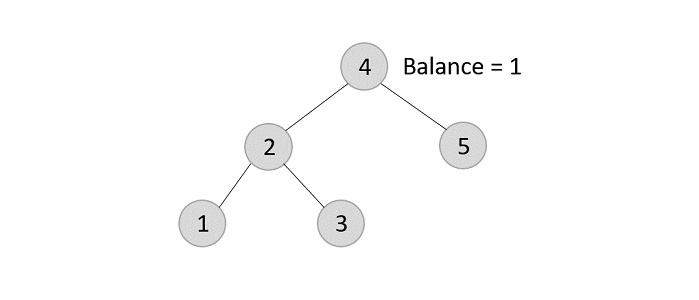
• Deleting element 6 from the output tree achieved −

However, element 6 is not a leaf node and has one child node attached to it. In this case, we replace node 6 with its child node: node 5.

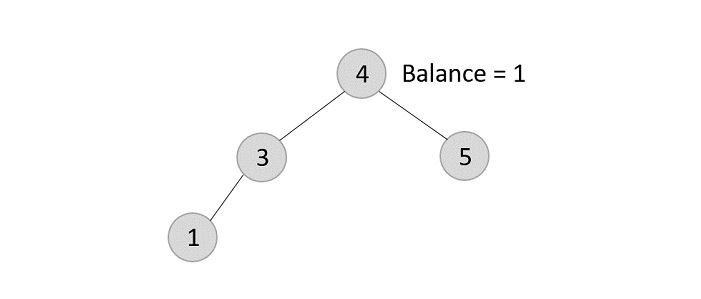
The balance of the tree becomes 1, and since it does not exceed 1 the tree is left as it is. If we delete the element 5 further, we would have to apply the left rotations; either LL or LR since the imbalance occurs at both 1-2-4 and 3-2-4.

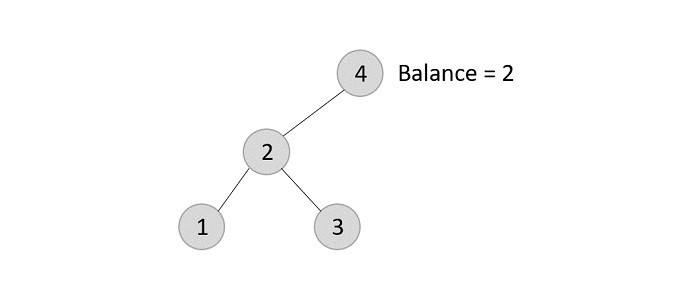
The balance factor is disturbed after deleting the element 5, therefore we apply LL rotation (we can also apply the LR rotation here).

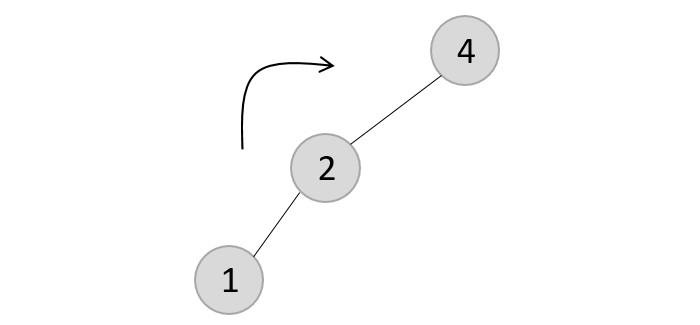
Once the LL rotation is applied on path 1-2-4, the node 3 remains as it was supposed to be the right child of node 2 (which is now occupied by node 4). Hence, the node is added to the right subtree of the node 2 and as the left child of the node 4.

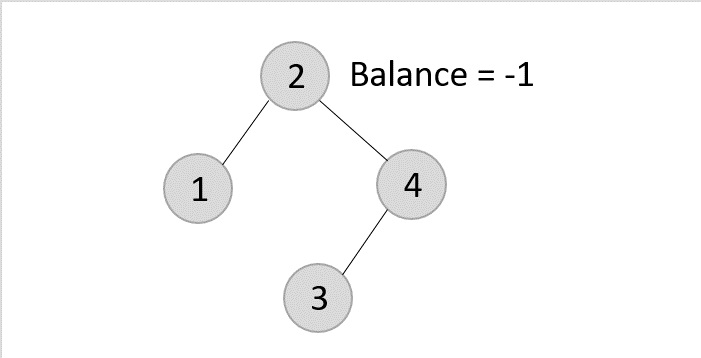
• Deleting element 2 from the remaining tree −

As mentioned in scenario 3, this node has two children. Therefore, we find its inorder successor that is a leaf node (say, 3) and replace its value with the inorder successor.

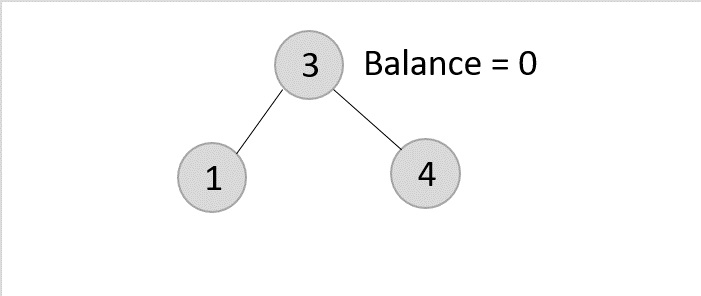
The balance of the tree still remains 1, therefore we leave the tree as it is without performing any rotations.