Tries Data Structure

A trie is a type of a multi-way search tree, which is fundamentally used to retrieve specific keys from a string or a set of strings. It stores the data in an ordered efficient way since it uses pointers to every letter within the alphabet.

The trie data structure works based on the common prefixes of strings. The root node can have any number of nodes considering the amount of strings present in the set. The root of a trie does not contain any value except the pointers to its child nodes.

There are three types of trie data structures −

• Standard Tries
• Compressed Tries
• Suffix Tries

The real-world applications of trie include − autocorrect, text prediction, sentiment analysis and data sciences.

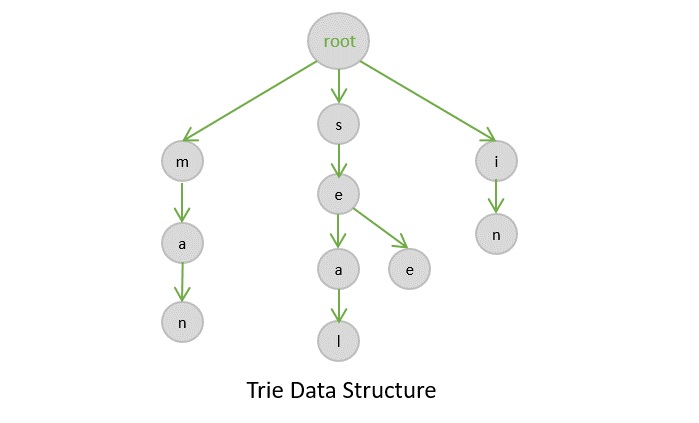
Basic Operations in Tries

The trie data structures also perform the same operations that tree data structures perform. They are −

• Insertion
• Deletion
• Search

Insertion operation

The insertion operation in a trie is a simple approach. The root in a trie does not hold any value and the insertion starts from the immediate child nodes of the root, which act like a key to their child nodes. However, we observe that each node in a trie represents a singlecharacter in the input string. Hence the characters are added into the tries one by one while the links in the trie act as pointers to the next level nodes.

Deletion operation

The deletion operation in a trie is performed using the bottom-up approach. The element is searched for in a trie and deleted, if found. However, there are some special scenarios that need to be kept in mind while performing the deletion operation.

Case 1 − The key is unique − in this case, the entire key path is deleted from the node. (Unique key suggests that there is no other path that branches out from one path).

Case 2 − The key is not unique − the leaf nodes are updated. For example, if the key to be deleted is see but it is a prefix of another key seethe; we delete the see and change the Boolean values of t, h and e as false.

Case 3 − The key to be deleted already has a prefix − the values until the prefix are deleted and the prefix remains in the tree. For example, if the key to be deleted is heart but there is another key present he; so we delete a, r, and t until only he remains.

Search operation

Searching in a trie is a rather straightforward approach. We can only move down the levels of trie based on the key node (the nodes where insertion operation starts at). Searching is done until the end of the path is reached. If the element is found, search is successful; otherwise, search is prompted unsuccessful.

Heap Data Structure

Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. If α has child node β then −

key(α) ≥ key(β)

As the value of parent is greater than that of child, this property generates Max Heap. Based on this criteria, a heap can be of two types −

Min-Heap − Where the value of the root node is less than or equal to either of its children.

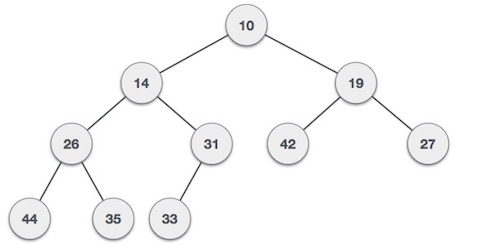
Max-Heap − Where the value of the root node is greater than or equal to either of its children.

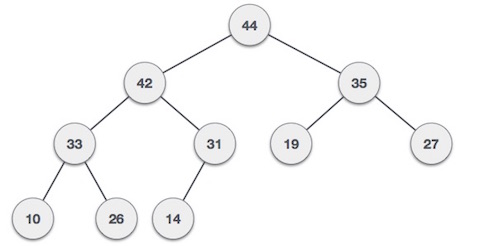
Both trees are constructed using the same input and order of arrival.

Max Heap Construction Algorithm

We shall use the same example to demonstrate how a Max Heap is created. The procedure to create Min Heap is similar but we go for min values instead of max values.

We are going to derive an algorithm for max heap by inserting one element at a time. At any point of time, heap must maintain its property. While insertion, we also assume that we are inserting a node in an already heapified tree.

Note − In Min Heap construction algorithm, we expect the value of the parent node to be less than that of the child node.

Let’s understand Max Heap construction by an animated illustration. We consider the same input sample that we used earlier.

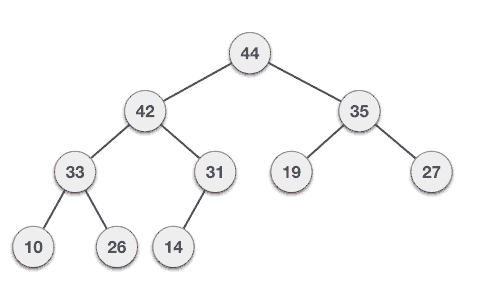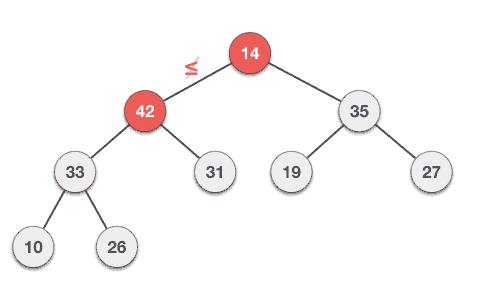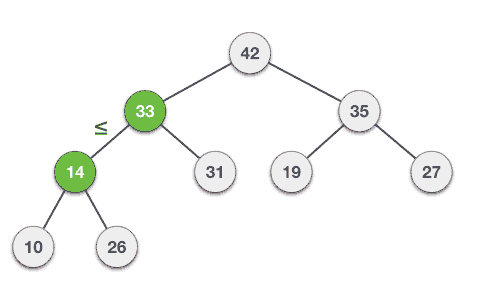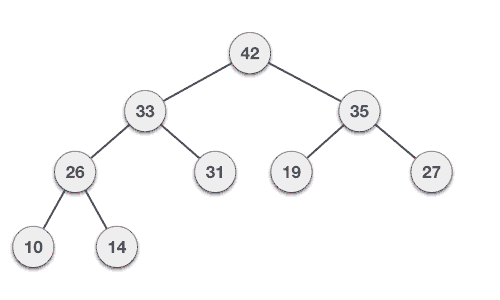
Max Heap Deletion Algorithm

Let us derive an algorithm to delete from max heap. Deletion in Max (or Min) Heap always happens at the root to remove the Maximum (or minimum) value.